昨晚(今早?)睡不着觉,就开始想下学期要学的概率论的那些事了,想着想着就想到了著名的山羊与汽车的问题。
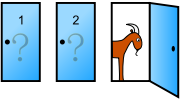
大意是这样,某电视节目里有这样的场景:三个门后面随机地放有两只山羊和一辆汽车。参赛者可以随机选出一扇门(当然目标是汽车不是山羊);当选手做出选择后,知道车具体在哪扇门后的主持人打开一扇后面有山羊的门。这是选手可以选择更换自己的选择或者不换。问题是,做出哪一个选择后更容易的到汽车呢?
大多数人都会这样思考问题:在主持人打开有山羊的门之前,选手拿到汽车的概率为1/3;而主持人排除一个错误选项后;相当于在两个里面随机抽一个,概率也就变成1/2了,因此换与不换的概率是一样的;都是1/2。昨晚我大概就是这么想的,但又知道答案是换比不换好,因而纠结了好久……
接下来我们试着编个程序来模拟下这个过程:
#include <stdio.h>
#include <math.h>
#include <time.h>
#include <stdlib.h>
#include <iostream>
using namespace std;
int main() {
int car,choice,change,no_change,open;
change=0;no_change=0;
int a[3],goat[2];
srand(time(NULL));
cout << "#tchoicetcartopentchangetno_changen";
for (int t=0;t<500;t++){
for (int i=0;i<3;i++) a[i]=0;
choice = rand()%3;
car = rand()%3;
a[car] = 1;
goat[0] = (car+1)%3;
goat[1] = (car+2)%3;
if (choice == car){
open = goat[rand()%2];
cout << t << "t" << choice+1 << "t" << car+1 << "t" << open+1 << "tt*n";
no_change++;
}
else{ // choice <> car
if (choice == goat[0]) open = goat[1];
else open = goat[0];
cout << t << "t" << choice+1 << "t" << car+1 << "t" << open+1 << "t*n";
change++;
}
}
cout << "============================n" << "Sum: n" << "Change: " << change << "nNo_change: " << no_change << "n";
}
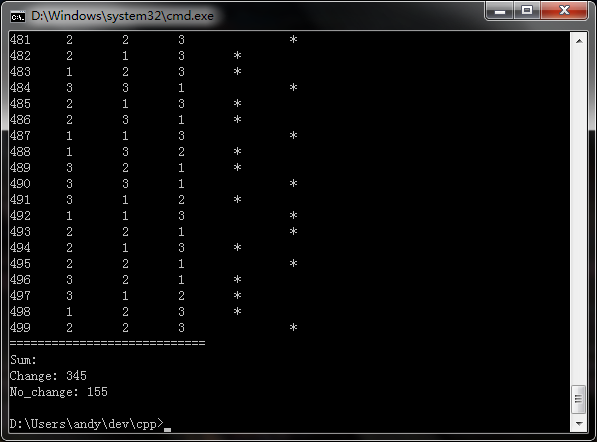
我设置的模拟次数是500,结果表示,换选项成功345次,不换成功155次。具体结果参见下面链接。
接着做两个解释:
1. 正确答案是什么
其实透过代码我们也可以知道这里应该分为两种情况讨论:
- 如果我们第一次就选中了汽车(这里的概率是 1/3),那么主持人会随机从两只山羊里选出一只。这是显然如果换了就错过汽车了,应该不换;
- 如果我们第一次选择山羊(这个概率为2/3),那么主持人一定会打开另一删后面有山羊的门;这是剩下最后一扇门后面就一定是汽车。这时更换选项就会成功。
因此,更换是否成功完全在于第一次是否选错,那么概率也就是 2/3。
2. 为什么 1/2 是错误的
这里我们可以再回到上面看一下那个通俗的错误解释。“主持人排除一个错误选项后;相当于在两个里面随机抽一个,概率也就变成 1/2 了” 而实际上,这里显然选手没有再次做随机选择的能力,而只是选择“换”或者是“不换”。比如说,如果参赛者知道答案,它第一次一定能选中汽车的话,那么第二次机会即使看起来是“在两个里面随机抽一个”,不换的概率就是1;而不是1/2。可以说,这个错误的解释里混淆了概率与结果。
如果还是很难理解的话,可以把问题抽象成小球并扩展到 5 (n) 个。假设有 4 个白球 1 个黑球,当随机抽出一个后,确定地拿出 3 (n-2) 个白球。那么剩下的那个没被拿走的球是黑球的概率不就是第一次抽到白球的概率,也就是 4/5 (1-1/n)了。
这个问题也有人叫做玛丽莲问题,因为这个问题是因为世界上智商最高的人玛丽莲给出了违反直觉的正确解答后才引起广泛的讨论的。这里是她的网站上记录的讨论,可以看到无数的 PhD 倒在的这里……